Algorytm

Euklidesa :

Algorytm wyznaczania największego dzielnika dwóch liczb całkowitych. Został on podany przez matematyka greckiego Euklidesa (ok. 365 -- ok. 300 p.n.e.) w jego fundamentalnym dziele Elementy. Uznawany za pierwszy algorytm, chociaż na terenach obecnych Chin i Indii znane były wcześniej inne przepisy na wykonywanie obliczeń. Do czasów ery komputerowej, a więc do połowy XX wieku, algorytm Euklidesa uchodził za synonim algorytmu.

PRZYKŁAD:

Dane są dwie liczby naturalne a i b.
1. Jeśli b ≠ 0 oblicz c jako resztę z dzielenia a przez b i zastąp a przez b, zaś b przez c.
2. Jeżeli b = 0, NWD wynosi a, w przeciwnym wypadku wróć do punktu pierwszego i kontynuuj.

Nasuwa się pytanie, czy takie postępowanie zawsze się skończy. Istotnie dla liczb naturalnych zawsze tak jest. Korzyść z algorytmu Euklidesa jest taka, że ostatnia niezerowa reszta jest, co łatwo sprawdzić jest największym wspólnym dzielnikiem liczb a i b.

Przykład
243 : 111 = 2, reszty 21
111 : 21 = 5, reszty 6
21 : 6 = 3, reszty 3
6 : 3 = 2, reszty 0
Ostatnia niezerowa reszta wynosi 3.
NWD(243, 111) = 3

Lioniowy :

Algorytm, którego wszystkie kroki można ustawić jeden po drugim i w takiej właśnie kolejności są wykonywane. Taki algorytm nie zawiera więc ani iteracji, ani kroków warunkowych (czyli rozgałęzień). Przykładem algorytmu liniowego jest sposób obliczania wartości konkretnego wyrażenia.

PRZYKŁADY :

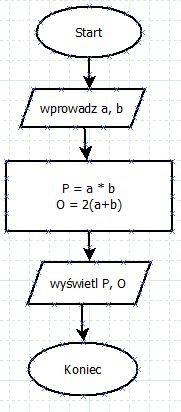
Przykładem algorytmu liniowego może być dowolny zestaw poleceń, które zawsze będą wykonywane jedna po drugiej i w przewidzianej kolejności. Reasumując bez żadnych warunków, iteracji, skoków etc.


Może to być algorytm obliczający średnią arytmetyczną podanych liczb:
Dane wejściowe: trzy liczby a, b, c.
Dane wyjściowe: liczba srednia, będąca średnią arytmetyczną tych liczb.

1. Start
2. Wczytaj a, b, c
3. srednia:=(a+b+c)/3
4. Wypisz srednia
5. Koniec.
 

Newtona-Raphsona :

Algorytm służący do obliczania wartości pierwiastka kwadratowego metodą iteracyjną. Dla danej liczby podpierwiastkowej a, obliczenia wartości sqrt(a) rozpoczynają się od wartości początkowej x0, która jest przybliżeniem rozwiązania, za którą można przyjąć na przykład (1+a)/2. Następne przybliżenia są wyznaczane ze wzoru:

xi+1 = (xi+a/xi)/2.

Obliczenia kończą się, gdy dwa kolejne przybliżenia niewiele różnią się między sobą, czyli gdy różnica |xi - xi+1| jest małą liczbą, na przykład 0.000001.

PRZYKŁAD :